SymPy Library: A Comprehensive Guide for Beginners

There is no getting around mathematics, whether you are a university student or work in data science.

One might even argue that data science is a type of applied mathematics/statistics. NumPy, SciPy, Scikit-Learn, and TensorFlow are just a few of the Python libraries that deal with mathematics quantitatively.

However, there is just one competitor for explicitly dealing with mathematical symbols: SymPy.

Let’s find out all about SymPy.

What is SymPy?

SymPy is a Python symbolic mathematics library. It aspires to be a full-featured computer algebra system (CAS) while keeping the code as basic as possible to be understandable and easily expandable.

It is fully written in Python. It is simple to use since it only relies on mpmath, a pure Python library for arbitrary floating-point arithmetic.

As a library, it was created with a significant emphasis on usability in mind. Extensibility is critical in the design of its application program interface (API).

As a result, it makes no attempt to enhance the Python language. The objective is for users to be able to use it  alongside other Python libraries in their workflow, whether in an interactive environment or as a programed component of a larger system.

SymPy, as a library, lacks a built-in graphical user interface (GUI). The library is:

• Free, both regarding speech and beer, because it is licensed under the BSD license.
• Python-based: It is totally developed in Python and employs Python as its language.
• Lightweight because it only relies on mpmath, a pure Python library for arbitrary floating-point arithmetic, making it simple to use.
• Can be incorporated into other programs and modified with custom functions in addition to being used as an interactive tool.

Why use SymPy?

Sage, a computer algebra system, also employs Python as its programming language. Sage, on the other hand, is enormous, requiring a download of more than a gigabyte. It has the benefit of being lightweight.

In addition to being compact, it has no dependencies other than Python, allowing it to be used practically everywhere.

Furthermore, the aims of Sage and SymPy are not the same. Sage aspires to be a full-featured mathematics system, and it does so by combining all of the main open-source mathematical systems into one.

When you use a Sage function, such as integrate, it invokes one of the open-source packages that it contains. In reality, it is built into Sage. SymPy, on the other hand, aspires to be a self-contained system, with all functionality implemented in it itself.

Its capacity to function as a library is an important feature. Many computer algebra systems are meant to be used in interactive environments, but they are difficult to automate or expand.

It can be used interactively in Python or imported into your own Python program. It also has APIs for easy extending it with your own routines.

Installing SymPy

Simply use the command below to install in your environment.

SymPy Symbols

Let’s get started with it now! Its fundamental object is a symbol. In SymPy, you can generate a symbol x by writing:

The code above generates the symbol x. Symbols in it are intended to emulate mathematical symbols that represent unknown values.

As a result, the following computation is shown below:

As shown above, the symbol x functions similarly to an unknown amount. If you wish to make many symbols, write them as follows:

You created two symbols, y, and z, at the same moment in this case. These symbols can now be added, subtracted, multiplied, and divided as wanted:

SymPy Functions

1. sympify() function

The sympify() method transforms an arbitrary expression into a SymPy expression. It converts standard Python objects, such as integers.

Strings are transformed to their expressions as well as integers, etc.

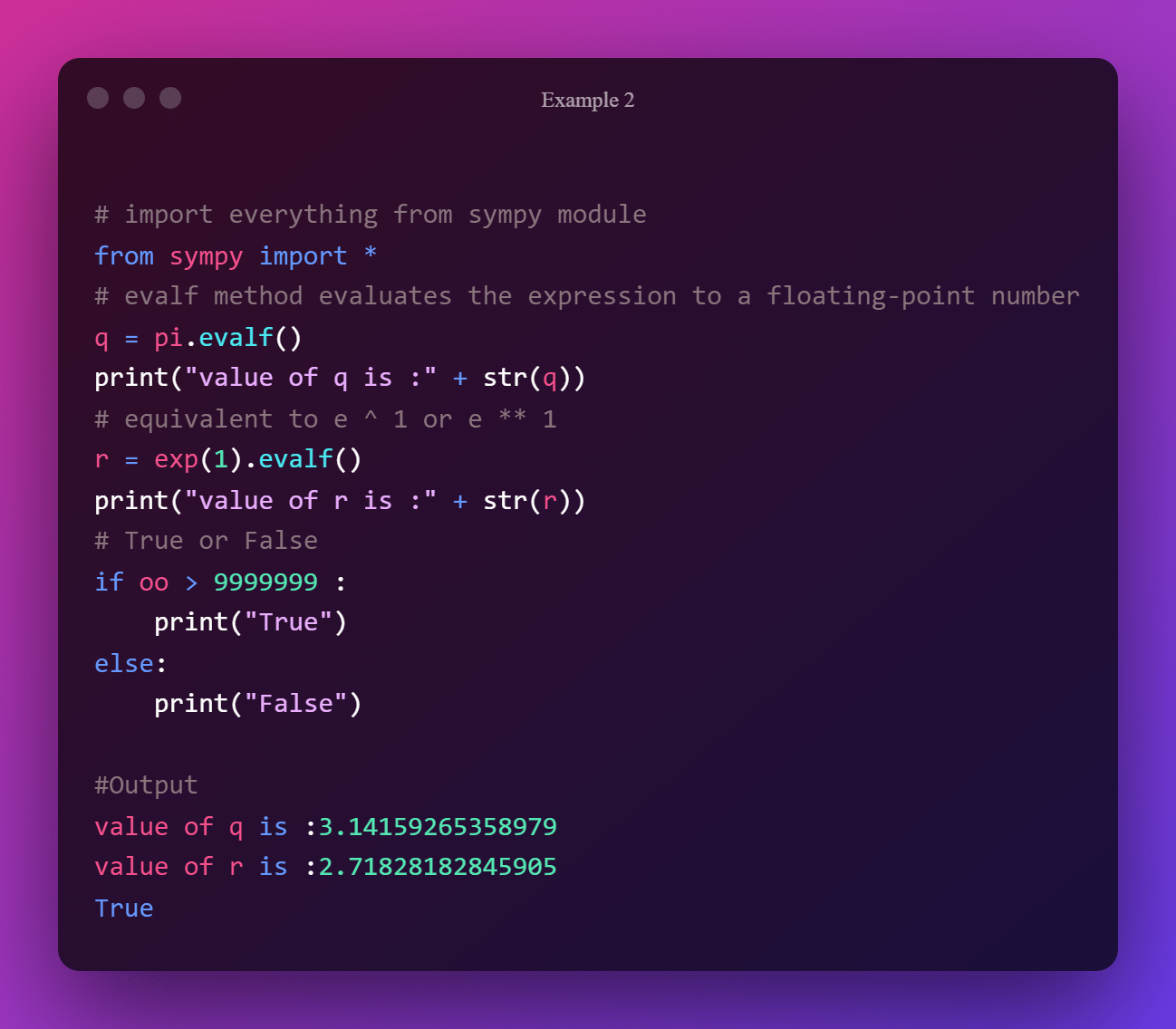
2. evalf() function

This function evaluates a specified numerical expression with a floating-point precision of up to 100 digits.

The function additionally accepts a dictionary object with numerical values for symbols as a subs argument. Consider the following phrase:

Floating-point accuracy is set to 15 digits by default. However, this can be changed to any number between 1 and 100.

The following equation is evaluated to a precision of 20 digits.

3. Lambdify() function

Lambdify is a function that converts its expressions into Python functions. The evalf() method is inefficient when evaluating an expression across a wide range of values.

Lambdify works similarly to a lambda function, except that it translates SymPy names to the names of the provided numerical library, which is generally NumPy.

By default, Lambdify is applied to math standard library implementations.

Features

A handful of the library’s most significant features are listed here; there are many more not included, but you can check them out here.

1. Core Capabilities

• Fundamental arithmetic: +, -, *, /, and ** operators are supported (power)
• A polynomial expansion
• Integers, rationals, and floats with arbitrary precision
• Trigonometric, hyperbolic, and exponential functions, roots, logarithms, absolute value, spherical harmonics, factorials and gamma functions, zeta functions, polynomials, and special functions
• Symbols that are non-commutative
• Matching patterns

2. Calculus

• Integration: This method employs the expanded Risch-Norman heuristic
• Differentiation.
• Limit functions
• Laurent Taylor’s series

3. Polynomials

• Gröbner foundations
• Decomposition of partial fractions
• Division, gcd Resultants are examples of basic arithmetic.

4. Combinatorics

• Permutations
• Gray and Prufer Codes
• Combinations, Partitions, Subsets
• Polyhedral, Rubik, Symmetric, and Other Permutation Groups

5. Discrete Maths

• Summations
• Logical expressions
• Binomial coefficients
• Number theory

Applications

1. Building Calculator

2. Computer Algebra Systems

Unlike other Computer Algebra Systems, you must manually declare symbolic variables in it using the Symbol() function.

3. Calculus

The capacity of a symbolic computation system to do all sorts of computations symbolically is its major strength.

It can simplify statements, symbolically, compute derivatives, integrals, and limits, solve equations, interact with matrices, and do a lot more.

To whet your appetite, here’s a taste of symbolic power.

What Else Can You Do With SymPy?

Rather than droning on about additional issues in-depth, let me provide you with a list of resources to help you enhance your skills:

• Matrices and Linear Algebra: It can work with matrices and perform basic linear algebra operations. The language is similar to NumPy’s syntax. However, there are notable differences. To begin, investigate matrices in library.
• Expression: It leverages an expression tree, which is a tree-based structure, to keep track of expressions. Look at expression trees if you want to learn more about their inner workings.
• Derivatives and Integrals: It can accomplish most of what you’d learn in an introductory calculus class (minus the thinking). You can begin by looking at our function differentiation in SymPy.
• Relationship with NumPy: NumPy and SymPy are both mathematics-related libraries. They are, nevertheless, essentially different! NumPy works with numbers, whereas it works with symbolic expressions.
• Simplifications: It is intelligent enough to automatically simplify expressions. However, if you want more fine-grained control over this, look at its simplifications.

Conclusion

SymPy is a powerful library for symbolic mathematics.

You can use it to create variables and functions, as well as symbolically extend and simplify mathematical statements and solve equations, inequalities, and even systems of equations/inequalities.

You can write the functions both in the script’s text and directly in the terminal (or Jupyter notebooks) to get a quick assessment and a better graphical depiction of the computations done.

Are you ready to explore more of SymPy? Let us know in the comments.