Matrix multiplication is a fundamental operation in linear algebra.
We generally use it in numerous applications such as image processing, machine learning, and many more. NumPy is a notable Python package for scientific computing.
However, in this post, we will look at various methods for doing matrix multiplication in Python without utilizing NumPy.
We will utilize nested loops, the built-in map() function, and list comprehension.
In addition, we will look at the benefits and drawbacks of each strategy, as well as when to apply each of them. If you are new to linear algebra and want to learn more about matrix multiplication; keep on reading.
Where Do We Use Matrix Multiplication?
Matrix multiplication is used in computer graphics to alter 2D and 3D visuals. For example, you can rotate, scale, and translate objects on the screen. Matrixes are used in image processing to represent pictures as arrays of pixels. Besides, matrixes may be used to conduct operations like image filtering.
We also make use of matrixes in machine learning. They can help us to represent data and model parameters. We can conduct numerous operations, such as computing dot products and matrix-vector products.
Surely, this operation is also highly advantageous in scientific operations. We can use it in physics and engineering to describe physical quantities. Hence, we can operate with vectors and tensors.
Why We May Not Choose to Use NumPy?
While NumPy is a Python library, it is not always the ideal option for matrix multiplication. We may not choose to use NumPy for reasons like size and dependency, learning, and legacy systems.
Using Python’s built-in functions or developing custom code may be more efficient in some instances. It is crucial to note, however, that NumPy is a strong library. Besides, you can also use it for matrix multiplication.
Now, let’s take a look at how can we achieve matrix multiplication without NumPy.
Nested loops method
The nested loops technique uses nested loops to execute matrix multiplication in Python. The function iterates over each matrix element. And, it multiplies them using a series of nested loops. The function returns the result, which is stored in a new matrix.
This approach is straightforward to grasp. However, it may not be as efficient as other ways, particularly for bigger matrices. Yet, it’s a wonderful choice for you if you are new to linear algebra.
def matrix_multiplication(A, B):
# Determine the matrices' dimensions.
rows_A = len(A)
cols_A = len(A[0])
rows_B = len(B)
cols_B = len(B[0])
# Set the result matrix to zeroes.
result = [[0 for row in range(cols_B)] for col in
range(rows_A)]
# Iterate through rows of A
for s in range(rows_A):
# Iterate through columns of B
for j in range(cols_B):
# Iterate through rows of B
for k in range(cols_A):
result[s][j] += A[s][k] * B[k][j]
return result
Let’s have an example of how to do this. You can just add these lines of code below to test this example.
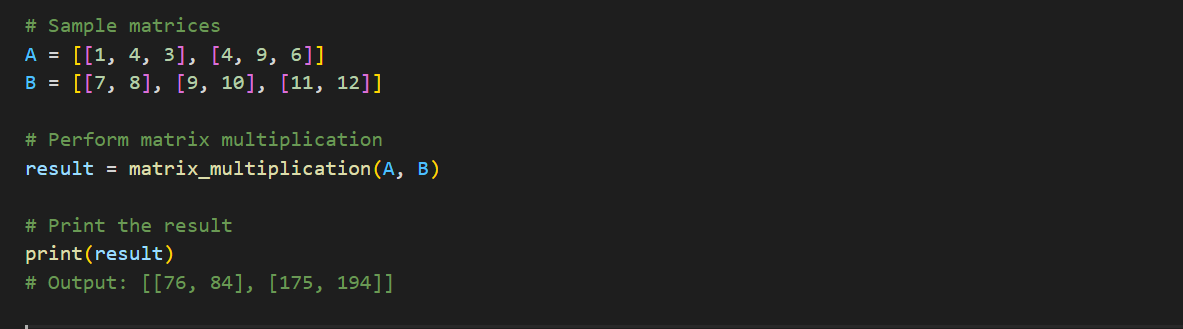
# Sample matrices
A = [[1, 4, 3], [4, 9, 6]]
B = [[7, 8], [9, 10], [11, 12]]
# Perform matrix multiplication
result = matrix_multiplication(A, B)
# Print the result
print(result)
# Output: [[76, 84], [175, 194]]
Benefits:
- Easy to comprehend.
- Great for newbies or those seeking a deeper comprehension of matrix multiplication.
Disadvantages:
- Not as effective as alternative techniques, particularly for bigger matrices.
- It is not as readable as alternate approaches.
map() function method
The map() function method provides an alternate approach for doing matrix multiplication in Python. In this approach, we use the built-in map() function. Hence, we use a functional programming tool that applies a provided function to each iterable element (list, tuple, etc.). Also, The map() function accepts two parameters, a function and an iterable. And, it returns an iterator that applies the function to each iterable element.
In this approach, we go through each member of the matrix and do the multiplication using the nested map() function.
The zip() function is used to iterate through each element of the matrices in parallel.
Finally, the sum() function is used to add up the results.
def matrix_multiplication(A, B):
# To get the dimensions of the matrices
rows_A = len(A)
cols_A = len(A[0])
rows_B = len(B)
cols_B = len(B[0])
# We use map() function for multiplication.
result = [[sum(a * b for a, b in zip(row_a, col_b)) for
col_b in zip(*B)] for row_a in A]
return result
Now, again, we can test our code with an example.
# Example matrices
A = [[3, 2, 3], [4, 5, 6]]
B = [[7, 8], [9, 10], [11, 12]]
# Use map() function to perform matrix multiplication
result = list(map(lambda x: list(map(lambda y: sum(i*j
for i,j in zip(x,y)), zip(*B))), A))
# Print the result
print(result)
# Output: [[72, 80], [139, 154]]
Advantages
- More effective than the stacked loops approach
- It uses functional programming to make the code simpler.
Disadvantages
- Some folks who are not familiar with functional programming may find it less readable.
- It is less understandable than the nested loops technique.
List comprehension method
List comprehension enables you to generate a new list in a single line of code. Hence, this is by applying an expression to each member of an existing list.
In this approach, multiplication is carried out by repeatedly iterating through each matrix member. We are using layered list comprehension.
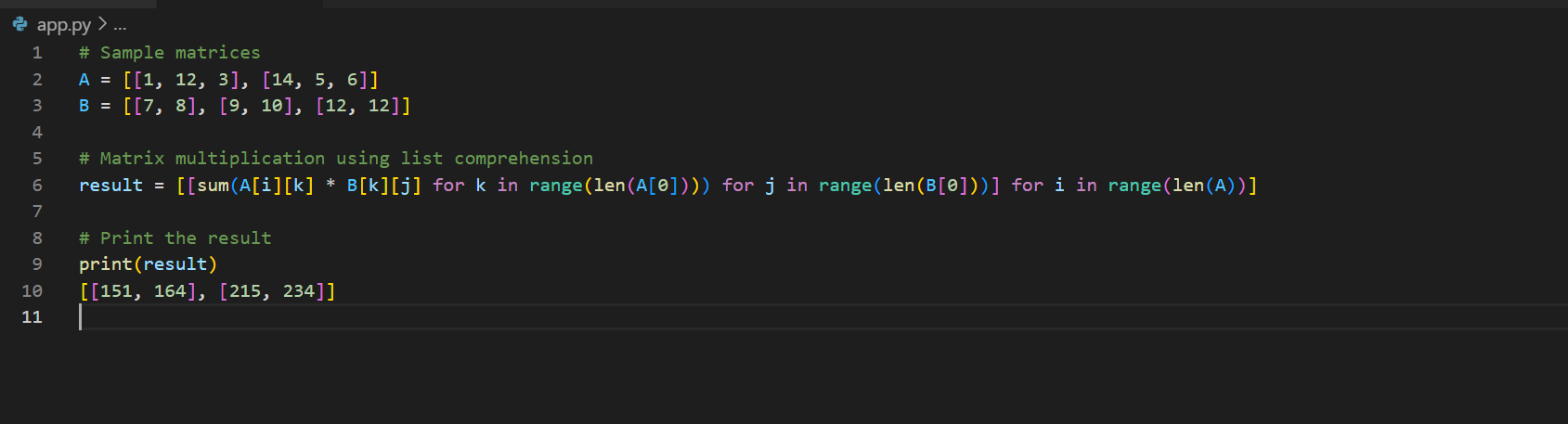
# Sample matrices
A = [[1, 12, 3], [14, 5, 6]]
B = [[7, 8], [9, 10], [12, 12]]
# Matrix multiplication using list comprehension
result = [[sum(A[i][k] * B[k][j] for k in range(len(A[0])))
for j in range(len(B[0]))] for i in range(len(A))]
# Print the result
print(result)
[[151, 164], [215, 234]]
Benefits
- Compared to the map() function method, shorter and more readable.
Disadvantages
- It may be less effective than using the map() function, particularly for large matrices.
- It is more difficult than the nested loops approach.
Conclusion
In this post, we looked at alternatives to using NumPy when multiplying matrices in Python. We performed matrix multiplication in nested loops, the built-in map() function, and list comprehension.
The best strategy will rely on the particular needs of your project.
Each of the strategies has pros and cons of its own. To make sure the function is operating properly, it’s a good idea to add some test cases with various matrix dimensions and values.
You should also include some performance tests to compare how well these methods execute.





Leave a Reply