We face optimization problems in many real-world circumstances where we need to identify the minimum or maximum of a function.
Consider a function to be a mathematical representation of a system, and determining its minimum or maximum can be critical for a variety of applications such as machine learning, engineering, finance, and others.
Consider a landscape with hills and valleys, and our goal is to find the lowest point (minimum) to get to our destination as quickly as possible.
We frequently use gradient descent algorithms to solve such optimization challenges. These algorithms are iterative optimization methods for minimizing a function by taking steps in the direction of the steepest descent (negative gradient).
The gradient reflects the direction with the steepest increase in the function, and traveling in the opposite direction leads us to the minimum.
What exactly is the Gradient Descent Algorithm?
Gradient descent is a popular iterative optimization approach for determining the minimum (or maximum) of a function.
It is a critical tool in several fields, including machine learning, deep learning, artificial intelligence, engineering, and finance.
The algorithm’s basic principle is based on its use of the gradient, which displays the direction of the sharpest increase in the function’s value.
The algorithm efficiently navigates the function’s landscape towards the minimum by repeatedly taking steps in the opposite direction as the gradient, iteratively refining the solution until convergence.
Why do We Use Gradient Descent Algorithms?
For starters, they can be used to solve a broad variety of optimization problems, including those with high-dimensional spaces and complex functions.
Second, they can find optimal solutions quickly, especially when the analytical solution is unavailable or computationally expensive.
Gradient descent techniques are highly scalable and can successfully handle enormous datasets.
As a result, they’re widely used in machine learning algorithms like training neural networks to learn from data and modify their parameters to minimize prediction mistakes.
A Detailed Example of Gradient Descent Steps
Let’s look at a more detailed example to have a better understanding of the gradient descent technique.
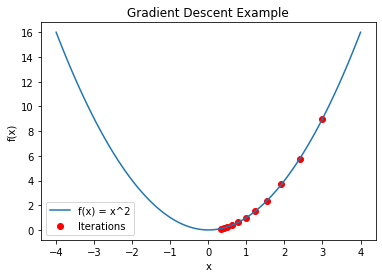
Consider the 2D function f(x) = x2, which generates a basic parabolic curve with a minimum at (0,0). The gradient descent algorithm will be used to determine this minimal point.
Step 1: Initialization
The gradient descent algorithm begins by initializing the value of the variable x, represented as x0.
The initial value can have a considerable impact on the algorithm’s performance.
Random initialization or employing prior knowledge of the problem are two common techniques. Assume that x₀ = 3 at the start of our case.
Step 2: Calculate the Gradient
The gradient of the function f(x) at the present position x₀. must then be calculated.
The gradient indicates the slope or rate of change of the function at that particular position.
We compute the derivative concerning x for the function f(x) = x2, which provides f'(x) = 2x. We get the gradient at x0 as 2 * 3 = 6 by substituting x₀ = 3 into the gradient calculation.
Step 3: Update Parameters
Using the gradient information, we update the value of x as follows: x = x₀ – α * f'(x₀), where α (alpha) denotes the learning rate.
The learning rate is a hyperparameter that determines the size of each step in the updating process. Setting an appropriate learning rate is crucial since a slow learning rate can cause the algorithm to take too many repetitions to reach the minimum.
A high learning rate, on the other hand, can result in the algorithm bouncing or failing to converge. Let us assume a learning rate of α = 0.1 for the sake of this example.
Step 4: Iterate
After we have the updated value of x, we repeat Steps 2 and 3 for a predetermined number of iterations or until the change in x becomes minimal, indicating convergence.
The method calculates the gradient, updates the value of x, and continues the procedure at each iteration, allowing it to get closer to the minimum.
Step 5: Convergence
The technique converges after a few iterations to a point where further updates do not materially impact the function’s value.
In our case, as the iterations continue, x will approach 0, which is the minimum value of f(x) = x^2. The number of iterations necessary for convergence is determined by factors such as the learning rate selected and the complexity of the function being optimized.
Choosing a Learning Rate ()
Choosing an acceptable learning rate () is critical for the gradient descent algorithm’s effectiveness. As previously stated, a low learning rate can induce slow convergence, whereas a high learning rate can cause overshooting and failure to converge.
Finding the proper balance is critical to ensuring that the algorithm converges to the intended minimum as efficiently as possible.
Tuning the learning rate is frequently a trial-and-error procedure in practice. Researchers and practitioners routinely experiment with different learning rates to see how they affect the algorithm’s convergence on their particular challenge.
Handling Non-Convex Functions
While the preceding example had a simple convex function, many real-world optimization issues involve non-convex functions with many local minima.
When utilizing gradient descent in such cases, the method can converge to a local minimum rather than the global minimum.
Several advanced forms of gradient descent have been developed to overcome this issue. Stochastic Gradient Descent (SGD) is one such method that introduces randomness by picking a random subset of data points (known as a mini-batch) to compute the gradient at each iteration.
This random sampling allows the algorithm to avoid local minima and explore new portions of the function’s terrain, boosting the chances of discovering a better minimum.
Adam (Adaptive Moment Estimation) is another prominent variation, which is an adaptive learning rate optimization approach that incorporates the benefits of both RMSprop and momentum.
Adam modifies the learning rate for each parameter dynamically based on previous gradient information, which might result in better convergence on non-convex functions.
These sophisticated gradient descent variations have proven to be effective in handling increasingly complex functions and have become standard tools in machine learning and deep learning, where non-convex optimization issues are common.
Step 6: Visualize Your Progress
Let’s see the progress of the gradient descent algorithm to get a better understanding of its iterative process. Consider a graph with an x-axis representing iterations and a y-axis representing the value of the function f(x).
As the algorithm iterates, the value of x approaches zero and, as a result, the function value drops with each step. When plotted on a graph, this would exhibit a distinct decreasing trend, reflecting the algorithm’s progress toward reaching the minimum.
Step 7: Fine-Tuning the Learning Rate
The learning rate () is an important factor in the algorithm’s performance. In practice, determining the ideal learning rate frequently necessitates trial and error.
Some optimization techniques, such as learning rate schedules, can alter the learning rate dynamically during training, starting with a higher value and gradually decreasing it as the algorithm approaches convergence.
This method helps to strike a balance between rapid development in the beginning and stability near the end of the optimization process.
Another Example: Minimizing a Quadratic Function
Let’s look at another example to get a better understanding of gradient descent.
Consider the two-dimensional quadratic function g(x) = (x – 5)^2. At x = 5, this function likewise has a minimum. To find this minimum, we shall apply gradient descent.
1. Initialization: Let’s begin with x0 = 8 as our starting point.
2. Calculate the gradient of g(x): g'(x) = 2(x – 5). When we substitute x0 = 8, the gradient at x0 is 2 * (8 – 5) = 6.
3. With = 0.2 as our learning rate, we update x as follows: x = x₀ – α * g'(x₀) = 8 – 0.2 * 6 = 6.8.
4. Iterate: We repeat steps 2 and 3 as many times as necessary until convergence is reached. Each cycle brings x closer to 5, the minimal value of g(x) = (x – 5)2.
5. Convergence: The method will eventually converge to x = 5, which is the minimal value of g(x) = (x – 5)2.
Learning Rates Comparison
Let’s compare the convergence speed of gradient descent for different learning rates, say α = 0.1, α = 0.2, and α = 0.5 in our new example. We can see that a lower learning rate (e.g., = 0.1) will result in a longer convergence but a more accurate minimum.
A higher learning rate (e.g., = 0.5) will converge faster but can overshoot or oscillate about the minimum, resulting in poorer accuracy.
A Multimodal Example of Non-Convex Function Handling
Consider h(x) = sin(x) + 0.5x, a non-convex function.
There are several local minima and maxima for this function. Depending on the starting position and learning rate, we could converge to any of the local minima using standard gradient descent.
We can resolve this by using more advanced optimization techniques like Adam or stochastic gradient descent (SGD). These methods use adaptive learning rates or random sampling to explore different regions of the function’s landscape, increasing the likelihood of achieving a better minimum.
Conclusion
Gradient descent algorithms are powerful optimization tools that are widely used in a wide range of industries. They discover the lowest (or maximum) of a function by iteratively updating parameters based on the direction of the gradient.
Because of the algorithm’s iterative nature, it can handle high-dimensional spaces and complex functions, making it indispensable in machine learning and data processing.
Gradient descent can easily tackle real-world difficulties and greatly contribute to the growth of technology and data-driven decision-making by carefully selecting the learning rate and applying advanced variations such as stochastic gradient descent and Adam.





Leave a Reply